Hey, I’m back !
If you’ve been following my progress reports, it may seem that I’m not doing much, in view of the little code I show here.
Although I also feel lagging behind a bit, one thing I suspected since the beginning (and realized even more now) is that this project is much less about spending time twisting screws than understanding which screws should be twisted… If you know what I mean.
Even if we’re leveraging third-party tools to perform simulation work in Xcos, it’s necessary to have a clear idea of how they work, so that we can provide their routines the correct information and connect them properly inside Scilab’s code. That involves trying to wrap your head around documentation from different projects, and even reading the current implementation code to know the way it is supposed to be done.
On one side, we have automatically generated code for simulation of different dynamical systems, exposed through a common and defined FMI2 interface, already presented here. On the other hand, Xcos simulator takes, on each iteration step, state information from every Scicos block and shove it on one of the available SUNDIALS numerical solvers to update model outputs.
Differential/algebraic equations
Depending on the type of solver used, mathematical representation of the model could assume 2 distinct formats: Ordinary Differential Equations (ODEs) or Differential-Algebraic Equations (DAEs).
Roughly speaking, ODEs are systems of equations that could be organized in the form:
With the state derivative x’ explicitly defined for every variable, given the current x value (which in turn is generally a function of the independent time variable t), numerical integration could be easily performed to obtain simulation results.
In cases where x’ is not known, can’t be expressed only in terms of t and x or there are numerical constraints involved, the model equations must be described in a more generalized DAE format:
That way, solving the system implies finding state derivatives that minimize F(t,x,x’) value, called residual. In other words, this method deals with approximate solutions.
DAEs could be converted to a system of coupled ODEs through index reduction, but solver calculations would be more costly than using a specific algorithm for index-1 DAEs. Thereby, it is interesting to support differential-algebraic solvers (e.g. IDA) as well as ordinary differential ones (CVODE, ARKode, etc.).
Scicos continuous state update jobs
For Scicos blocks computational function, there are 3 flags related to continuous time state updates:
| flags | inputs | outputs | description |
|---|---|---|---|
| 0 | t, nevprt, x, z, inptr, mode, phase | xd, res | compute the derivative of continuous time state |
| 1 | t, nevprt, x, z, inptr, mode, phase | outptr | compute the outputs of the block |
| ... | ... | ... | ... |
| 10 | t, nevprt, x, z, inptr, mode, phase | res | compute jacobian matrix |
(It’s worth noting that by “continuous” here I mean “not triggered by events”, as we can’t really have continuous change in a computer calculation, just discrete updates after regular time steps)
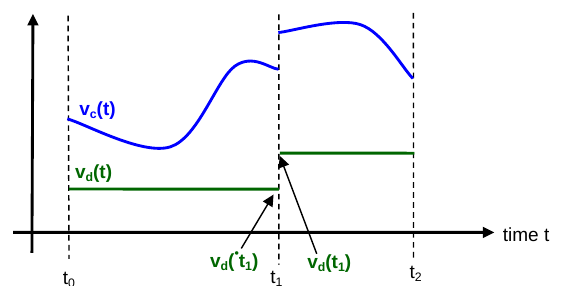
(Piecewise-continuous variables of an FMU: continuous-time (vc) and discrete-time (vd))
Jobs 0 and 1 are described in the documentation, respectively, as:
-
Integrator calls: This job is called when flag=0. In this case, the simulation function computes the derivative state x_dot and place its value in the address provided by the block’s structure.
-
This job is called when flag=1, it is called only if the block has regular ports. In this case, the simulator requests the values of the outputs. The computational function uses the information given by the block structure to calculate the output and put it at the address given by the block structure. If the block contains different mode then the calculation depends on the simulation phase.
At first, I couldn’t find information regarding job 10, that computes the Jacobian derivatives matrix used by some solvers. It was not mentioned in that document, and common (explicit) Scicos blocks do not implement it. So I had to look at blocks generated by current modelicac compiler to understand what it returns, e.g.:
void BouncingBall_Modelica_im(scicos_block *block, int flag)
{
double *rpar = block->rpar;
double *x = block->x;
double *xd = block->xd;
double **y = block->outptr;
double *res = block->res;
/* ... */
/* Intermediate variables */
double v0;
if (flag == DerivativeState) { // Flag 0
res[0] = xd[0]-x[1];
res[1] = rpar[0]+xd[1];
} else if (flag == OutputUpdate) { // Flag 1
if (get_phase_simulation() == 1) {
y[0][0] = x[0]; /* OutPutPort1.vo */
y[1][0] = x[1]; /* OutPutPort2.vo */
} else {
y[0][0] = x[0]; /* OutPutPort1.vo */
y[1][0] = x[1]; /* OutPutPort2.vo */
}
/* ... */
} else if (flag == Jacobian) { // Flag 10
v0 = Get_Jacobian_parameter();
res[0] = v0;
res[1] = 0.0;
res[2] = -1.0;
res[3] = v0;
res[4] = 1.0;
res[5] = 0.0;
res[6] = 0.0;
res[7] = 1.0;
set_block_error(0);
}
return;
}Where I found strange that, for either DerivativeState and Jacobian jobs, the residual res is being returned rather than xd. Further investigation led me to another design document that asserts:
-
block->xd: Array of doubles of size [nx,1] corresponding to the derivative of the continuous state register. It is an output of the simulation function if the block is an explicit block, i.e. the block models a system of Ordinary Differential Equations (ODE), otherwise, it is an input. In the latter case, the output is the residual vector res associated with a system of Differential Algebraic Equations (DAE).
-
block.xd: a vector of size nx giving the value of the derivative continuous state register. Values of the derivative continuous state register will be saved in the C structure of the block only for flag=4, flag=6, flag=0 and flag=2.
-
block.res: a vector of size nx corresponding to the Differential Algebraic Equation (DAE) residual. Values of that register will be saved in the C structure of the block only for flag=0, and flag=10
From that we can deduce that flag 0 has deal with xd input and res output or only xd output, while flag 10 will always output res. This is confirmed by inspecting the main simulator code, in scicos.c (not shown here for readability).
So, with things figured out, we can finally implement those jobs in our FMI2 wrapper:
/* Includes and definitions */
// Utility function for setting Scicos block -> FMI2 model input
static void set_input(scicos_block* block)
{
// Considering input only floating point continuous values
double** u = (double**) block->inptr;
// Set u inputs before calculation derivatives
if( block->nin > 0 )
{
for( int i = 0; i < block->nin; i++ )
inputsList[ i ] = u[ i ][ 0 ];
fmi2SetReal( (fmi2Component) block->work, INPUT_REFS_LIST, block->nin, inputsList );
}
}
// Utility function for getting FMI2 model -> Scicos block output
static void get_output(scicos_block* block)
{
// Considering output only floating point continuous values
double** y = (double**) block->outptr;
// Retrieve output values
if( fmi2GetReal( (fmi2Component) block->work, OUTPUT_REFS_LIST, block->nout, outputsList ) == fmi2OK )
{
// Setting outputs the same as continuous states
for( int i = 0; i < block->nout; i++ )
y[ i ][ 0 ] = outputsList[ i ];
}
}
/* ... */
SCICOS_IMPEXP void BLOCK_FUNCTION_NAME( cicos_block* block, const int flag )
{
switch (flag)
{
/* ... */
// Flag 0: Update continuous state
case DerivativeState:
{
fmi2SetTime( (fmi2Component) block->work, get_scicos_time() );
set_input( block );
// Get state time derivatives
fmi2GetDerivatives( (fmi2Component) block->work, stateDerivativesList, block->nx );
// Output both residuals for implicit (DAE) solvers
for( int i = 0; i < block->nx; i++ )
{
block->res[ i ] = stateDerivativesList[ i ] - block->xd[ i ];
}
break;
}
/* ... */
// Flag 1: Update output state
case OutputUpdate:
{
get_output( block );
break;
}
case Jacobian:
{
// (To be implemented)
break;
}
/* ... */
}
}Wow ! That was a rather long post. I hope it was enough to explain things for now.
Also sorry for the current rough implementation. I’m in a hurry with first GSoC evaluations, but I do plan to update the publication later with more detailed code.
Thanks for sticking with me one more time. See Ya !